
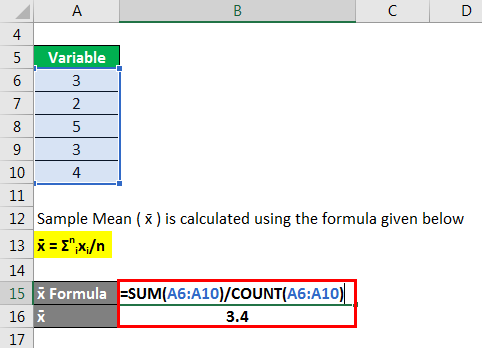
Matrix W 0 (range I2:K4) is calculated by the array formula The calculations continue as shown in Figure 2.įigure 2 – Finding HAC standard errors (part 2)
We first calculate the residuals (column G of Figure 1) as in Figure 3 of Breusch-Godfrey Test.įigure 1 – Finding HAC standard errors (part 1) We also add a column of ones in column A so that range A4:C23 is the design matrix. We repeat the data elements in columns B, C and D of Figure 1. V i as the n-i × k matrix consisting of the last n-i rows in XĮxample 1: Calculate the HAC standard errors for Example 1 of Breusch-Godfrey Test for order h = 3. U i as the n-i × k matrix consisting of the first n-i rows in X R i as the n-i × 1 column vector whose values are e 1 e i +1, e 2 e i +2, …, e n-ie n Note too that Newey-West not only corrects for autocorrelation it also corrects for heteroscedasticity (heterogeneity of variances). The Newey-West method handles autocorrelation with lags up to h, and so it is assumed that lags larger than h can be ignored. The first sum in the formula is the value of X TSX when there is no autocorrelation (i.e. Where X i is the i th row in the design matrix X. When there is autocorrelation with lags up to h > 0, we use the following value The standard errors that result are called Heteroskedasticity and Autocorrelation Corrected ( HAC) standard errors. The Newey-West method uses the same approach, except that X TSX is calculated in yet another way. This same approach is used in Huber-White’s Robust Standard Errors method where there isn’t homogeneity of variances, except that S is calculated in a different way. Where R is the column vector consisting of values. This can be estimated using the covariance matrix of the residuals, which is a diagonal matrix whose diagonal consists of the values n/( n-k) Where σ 2 is the common variance of the residuals ε i, as estimated by MSE. Images not copyright InfluentialPoints credit their source on web-pages attached via hypertext links from those images.In OLS regression, the regression coefficients are computed using In good agreement with both the (approximate) formula above - and with the estimated standard error for such a mean (using σ x/√n).įollowing an identical procedure, sampling a slightly skewed population, the standard deviation of their medians was only 1.19698 times the standard deviation - and when we sampled a highly skewed population, the standard deviation of their medians dropped to just 1/ 10 18 of the standard deviation of their means.Įxcept where otherwise specified, all text and images on this page are copyright InfluentialPoints, all rights reserved. Repeating this calculation 5000 times, we found the standard deviation of their 5000 medians (0.40645) was 1.25404 times the standard deviation of their means. Since the median is usually only used when the data are not drawn from a normally distributed population, this rather limits the usefulness of this formula, and it is rarely used.įor example, using R, it is simple enough to calculate the mean and median of 1000 observations selected at random from a normal population (μ x=0.1 & σ x=10). the sample is drawn from a normally distributed population.SE ( ) is the standard error of the mean.

SE (median) is the standard error of the median,.Providing certain assumptions are made, the standard error of the median can be estimated by multiplying the standard error of the mean by a constant:


 0 kommentar(er)
0 kommentar(er)
